Circuitos en paralelo de corriente alterna
      1. Circuito en paralelo RLC
      2. Método de las admitancias
      3. Caso particular de dos impedancias en paralelo
1. Circuito en paralelo RLC
    En un circuito RLC que presente los tres elementos conectados en paralelo, la tensión total aplicada al circuito es la misma que la que tenemos en bornes de cada elemento, mientras que la intensidad que circula para cada uno de ellos es distinta y depende de los efectos de la R,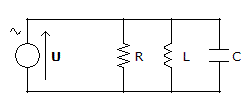 de la L y de la C.
Por tanto, la intensidad que circula por la resistencia está en fase con la tensión aplicada y su valor, que es independiente de la frecuencia, será:

Utilizando la notación compleja:

    La intensidad que circula por la bobina está retrasada π/2 respecto a la tensión aplicada y su valor está limitado por la reactancia inductiva XL, que es directamente proporcional a la frecuencia, siendo esta intensidad:

    Por la capacidad circula una intensidad que está adelantada π/2 respecto a la tensión y cuyo valor está limitado por la reactancia capacitiva XC, que es inversamente proporcional a la frecuencia, siendo:

    Y utilizando la notación compleja:

    Por tanto, aplicando la primera ley de Kirchoff y utilizando la notación compleja, la intensidad total que absorbe el circuito es:

    Teniendo en cuenta la ley de Ohm generalizada:

    Obtendremos la impedancia compleja del circuito:

    Siendo el módulo de la impedancia:

    Y el ángulo:

 

2. Método de las admitancias
    En los circuitos en paralelo de corriente alteña el cálculo se simplifica utilizando el concepto de admitancia.
La admitancia, Y, de un elemento o de una rama de un circuito es el cociente entra la intensidad que circula a través de dicho elemento o rama y la tensión aplicada entre sus extremos.

    La admitancia es la inversa de la impedancia.

    Siendo Ψ=-φ
    Escribiendo la impedancia en forma compleja:


    Donde G es la conductancia y B la susceptancia. Siendo:

    Y:

    La susceptacia será negativa si el circuito es inductivo y positiva si es capacitivo.
Admitancia, conductancia y susceptancia se miden en siemens (S)
Para un circuito con n impedancias en paralelo, aplicamos la ley de Ohm a cada rama y calculamos la intensidad total:

Como Y=1/Z, sustituimos y nos queda:

    Siendo la admitancia de entrada o equivalente y su unidad, el siemens.
    Para sumar las admitancias parciales se deben de expresar en su forma binómica:

    Para resolver los circuitos se convertirán las impedancias de todas las ramas en admitancias, luego se haya la admitancia equivalente y, por último, la impedancia total del circuito. Además podemos hallar las intensidades de cada una de las ramas utilizando la admitancia:

Triángulo de admitancias en circuito RLC paralelo
Esta unidad interactiva requiere la máquina virtual de Java J2RE.



Puedes introcucir los valores de R, C, U en los campos de texto de la parte inferior. También puedes  variar el valor de f en el cursor.


3. Caso particular de dos impedancias en paralelo
     Para un circuito formado por dos impedancias Z1 y Z2 sometidas a una tensión alterna de valor U, tendremos:
    Operando:


Índice
 Continuar